Working with polygons
At the core of each pyTDGL simulation is an instance of the tdgl.Device class, which represents the superconducting structure to be modeled. A Device is composed a Layer that lies in a plane parallel to the \(x-y\) plane (at position layer.z0) and has a specified thickness \(d\), coherence length \(\xi\) and London penetration depth \(\lambda\). The layer contains superconducting film, which can contain zero or more holes. Films and holes are
represented by instances of the tdgl.Polygon class, which defines a 2D polygonal region.
[1]:
%config InlineBackend.figure_formats = {"retina", "png"}
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import tdgl
A Polygon is defined by a collection of (x, y) coordinates specifying its vertices; the vertices are stored as an n x 2 numpy.ndarray called polygon.points.
[2]:
# Define the initial geometry: a rectangular box specified as an np.ndarray
width, height = 10, 2
points = tdgl.geometry.box(width, height)
print(f"type(points) = {type(points)}, points.shape = {points.shape}")
type(points) = <class 'numpy.ndarray'>, points.shape = (100, 2)
[3]:
# Create a Polygon representing a "horizontal bar", hbar
hbar = tdgl.Polygon(points=points)
hbar.polygon
[3]:
The object passed to tdgl.Polygon(points=...) can be of any of the following:
An
n x 2array-like object, for example annp.ndarrayor a list of(x, y)coordinatesAn existing
tdgl.Polygoninstance (in which case, the new object will be a copy of the existing one)An instance of LineString, LinearRing, or Polygon from the shapely package
[4]:
(
tdgl.Polygon(points=hbar.points)
== tdgl.Polygon(points=hbar.polygon)
== tdgl.Polygon(points=hbar)
== hbar.copy()
== hbar
)
[4]:
True
Every instance of tdgl.Polygon has a property, instance.polygon, which returns a corresponding shapely Polygon object. Among other things, this is usefuly for quickly visualizing polygons.
There are several methods for transforming the geometry of a single Polygon:
polygon.translate(dx=0, dy=0)polygon.rotate(degrees, origin=(0, 0))polygon.scale(xfact=1, yfact=1, origin=(0, 0))polygon.buffer(distance, ...)
There are also three methods for combining multiple Polygon-like objects:
polygon.union(*others): logical union ofpolygonwith each object in the iterableothersSee also:
tdgl.Polygon.from_union([...])polygon.intersection(*others): logical intersection ofpolygonwith each object in the iterableothersSee also:
tdgl.Polygon.from_intersection([...])polygon.difference(*others): logical difference ofpolygonwith each object in the iterableothersSee also:
tdgl.Polygon.from_difference([...])
Note that the elements of the iterable others can be of any type that can be passed in to tdgl.Polygon(points=...) (see above).
[5]:
# Copy hbar and rotate the copy 90 degrees counterclockwise
vbar = hbar.rotate(90)
vbar.polygon
[5]:
[6]:
# Create a new Polygon that is the union of hbar and vbar: "+"
plus = hbar.union(vbar)
# # The above is equivalent to either of the following:
# plus = vbar.union(hbar)
# plus = tdgl.Polygon.from_union([hbar, vbar])
plus.polygon
[6]:
[7]:
# Rotate the "+" by 45 degrees to make an "X"
X = plus.rotate(45)
X.polygon
[7]:
[8]:
# Create a new polygon with all edges offset (eroded) by a distance of -0.5
thinX = X.buffer(-0.5)
thinX.polygon
[8]:
[9]:
# Create a new polygon with all edges offset (expanded) by a distance of 0.5
thickX = X.buffer(0.5)
thickX.polygon
[9]:
[10]:
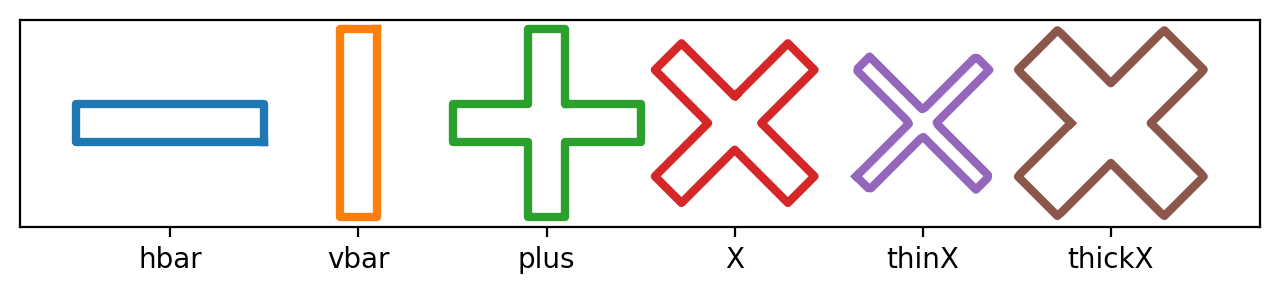
polygons = [hbar, vbar, plus, X, thinX, thickX]
labels = ["hbar", "vbar", "plus", "X", "thinX", "thickX"]
fig, ax = plt.subplots(figsize=(8, 1.5))
for i, polygon in enumerate(polygons):
polygon.translate(dx=width * i).plot(ax=ax, linewidth=3)
ax.set_xticks([width * i for i, _ in enumerate(labels)])
ax.set_xticklabels(labels)
_ = ax.set_yticks([])
[11]:
X.union(plus).polygon
[11]:
[12]:
X.intersection(plus).polygon
[12]:
Using the methods demonstrated above, intricate geometries can be constructed from simple building blocks in just a few lines of code.
[13]:
size = 10
hbar = tdgl.Polygon(points=tdgl.geometry.box(size / 3, size / 50))
plus = hbar.union(hbar.rotate(90))
star = plus.union(plus.rotate(45))
star_dx = 1.2 * size * np.sqrt(2) / 2
snowflake = (
tdgl.Polygon(points=tdgl.geometry.box(size, size))
.rotate(45)
.union(
*(star.translate(dx=star_dx).rotate(degrees) for degrees in [0, 90, 180, 270])
)
)
snowflake = snowflake.union(snowflake.rotate(45))
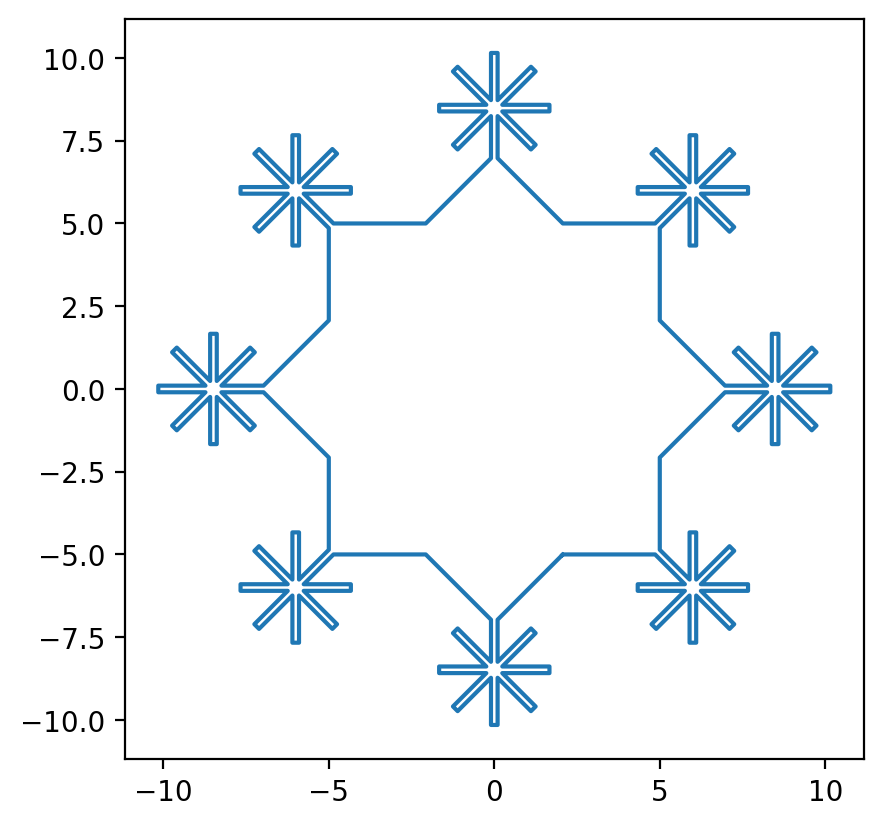
[14]:
ax = snowflake.plot()
[15]:
print(f"Polygon area: snowflake.area = {snowflake.area:.3f}")
print(f"Polygon width and height: snowflake.extents = {snowflake.extents}")
Polygon area: snowflake.area = 136.622
Polygon width and height: snowflake.extents = (20.303896081810475, 20.303896081810475)
Meshing Polygons
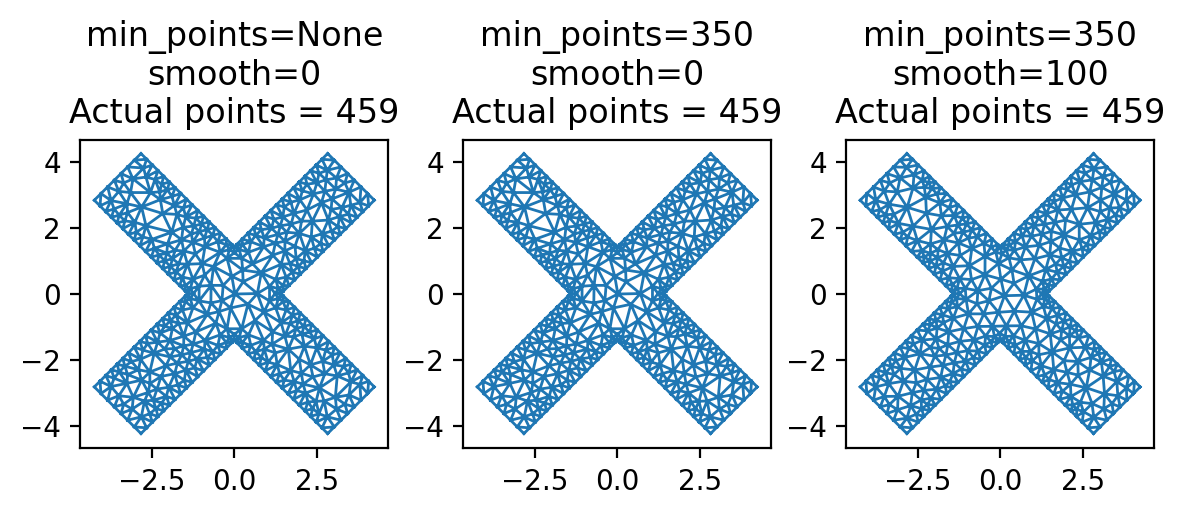
Individual polygons can be meshed using the Polygon.make_mesh() method.
[16]:
setups = [
dict(min_points=None, smooth=0),
dict(min_points=350, smooth=0),
dict(min_points=350, smooth=100),
]
fig, axes = plt.subplots(1, len(setups), figsize=(2 * (len(setups) + 0.5), 2))
for ax, options in zip(axes, setups):
# Generate a mesh with the specified options
mesh = X.make_mesh(**options)
# Plot the mesh
ax.set_aspect("equal")
title = [f"{key}={value!r}" for key, value in options.items()]
title.append(f"Actual points = {mesh.x.shape[0]}")
ax.triplot(mesh.x, mesh.y, mesh.elements, lw=1)
ax.set_title("\n".join(title))
Constructing Voronoi polygons: 100%|█████████████████████████████████████████████████████████████████████| 459/459 [00:00<00:00, 17015.81it/s]
Constructing Voronoi polygons: 100%|█████████████████████████████████████████████████████████████████████| 459/459 [00:00<00:00, 17668.90it/s]
Constructing Voronoi polygons: 100%|█████████████████████████████████████████████████████████████████████| 459/459 [00:00<00:00, 17594.46it/s]
[17]:
tdgl.version_table()
[17]:
| Software | Version |
|---|---|
| tdgl | 0.8.1; git revision 25e009d [2024-04-10] |
| Numpy | 1.24.3 |
| SciPy | 1.10.1 |
| matplotlib | 3.7.1 |
| cupy | None |
| numba | 0.57.1 |
| IPython | 8.14.0 |
| Python | 3.10.11 | packaged by conda-forge | (main, May 10 2023, 19:01:19) [Clang 14.0.6 ] |
| OS | posix [darwin] |
| Number of CPUs | Physical: 10, Logical: 10 |
| BLAS Info | OPENBLAS |
| Wed Apr 10 14:14:21 2024 PDT | |
[ ]: